Streamlines
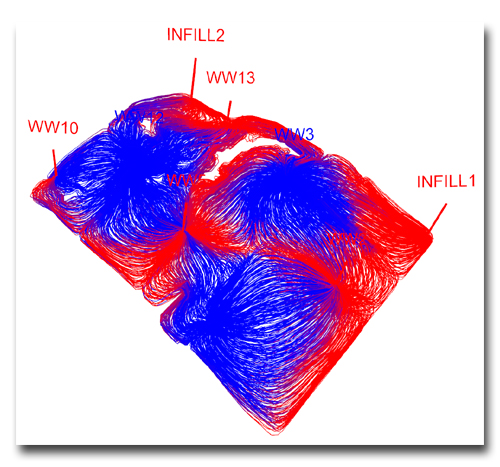
The key feature of streamline simulation is that fluids are transported over a time step (t to t+Δt) along streamlines, rather than moving cell-to-cell as in conventional Eulerian grid methods. Components are assumed to travel along streamlines until the velocity field is updated to reflect dynamic changes of the flow field over time. The geometry of the streamlines, as well as the velocity of phases and components traveling along them, is governed by the spatial distribution of static petrophysical properties (e.g., permeability, porosity, relative permeability regions) and the injection/production volumes at the wells. This ability to visualize flow is exceptionally intuitive, even for untrained observers.
The most significant advantage of streamline simulation compared to other methods lies in the insights provided by the streamlines themselves. Two particularly valuable sources of data include:
- Streamlines can delineate the drainage and irrigation volumes linked to producers and injectors, respectively. They make it possible to identify which grid blocks are associated with specific wells—whether injectors or producers—at any given time. These regions can be leveraged in well-level assisted history matching workflows to adjust static grid properties and improve the alignment between simulated and observed historical volumes. Additionally, they can serve as a metric to evaluate the effectiveness of upscaling methodologies. In streamline-based surveillance, the control volumes derived from streamlines associated with an injector or producer are used for material balance calculations.
- Summing the volumetric flow rates of all streamlines connecting an injector-producer pair enables the calculation of well rate allocation factors (WAFs), which represent the percentage of flow from one well to each offset well it communicates with. Streamlines provide the most rigorous solution to the complex challenge of linking produced and injected volumes. Well allocation data are essential for pattern analysis and effective flood management.
Streamlines have been in the literature for a long time. For one of the earliest papers on the subject see Morris Muskat's and Ralph Wyckoff's 1933 paper: A Theoretical Analysis of Water-flooding Networks, which is freely downloadable from the SPE website.
Drainage/Irrigation Volumes
Streamlines are unique in allowing determining drainage volumes associated with producers or irrigation volumes associated with injectors. Furthermore, since streamlines change with time it is possible to display and quantify the changing volumes associated with each well as well rates change and/or new wells come online.
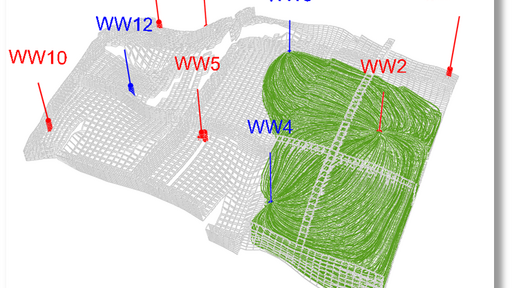
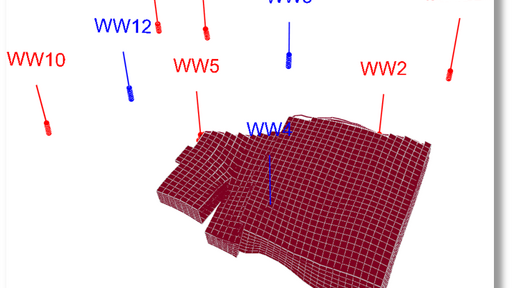
Streamlines connected to producer WW2 defining the drainage volume associated with the producer at that a particular moment in time.
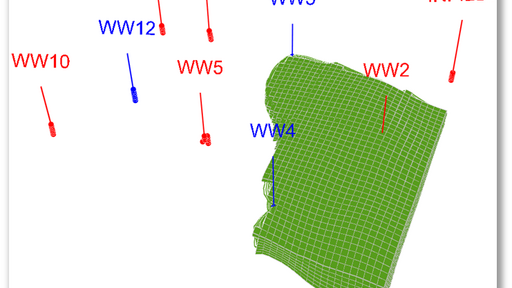
The drainage volume is found by finding all the gridblocks of the underlying static Eulerian grid that are being intersected by the all the streamlines associated with producer WW2.
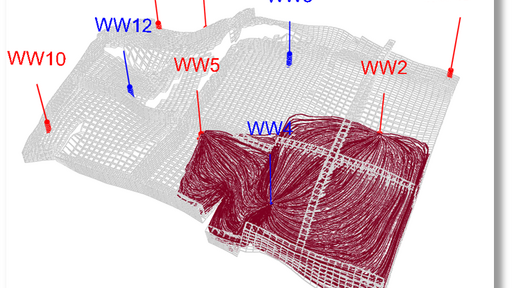
Streamlines connected to injector WW4 defining the irrigation volume associated with the injector at that a particular moment in time.
The irrigation volume is found by finding all the gridblocks of the underlying static Eulerian grid that are being intersected by the all the streamlines associated with injector WW4.
Flux Pattern Map (FPmap)
The Flux Pattern Map (FPmap) is a patented visualization technology by Streamsim (US Patent 6,519,531) designed to display and quantify connectivity between injector and producer pairs. In the FPmap, all streamlines linking a source/sink pair—typically an injector/producer pair—are schematically represented by edges. These edges use color, thickness, and labels to characterize individual connections, making it easy to quickly distinguish strong connections from weak ones.
This data, known as well-allocation factors (WAFs), plays a vital role in effective field management. WAFs change over time as streamlines are updated to reflect changes in well rates, the opening or closing of wells, or changes in the in-situ fluid distribution.
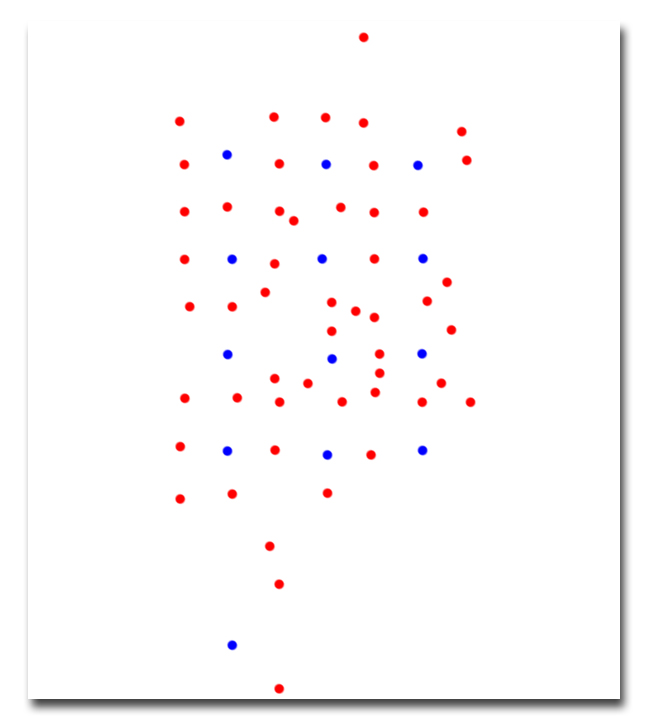
Red dots represent open producers and blue dots open injectors as seen from above at a partiuclar moment in time.
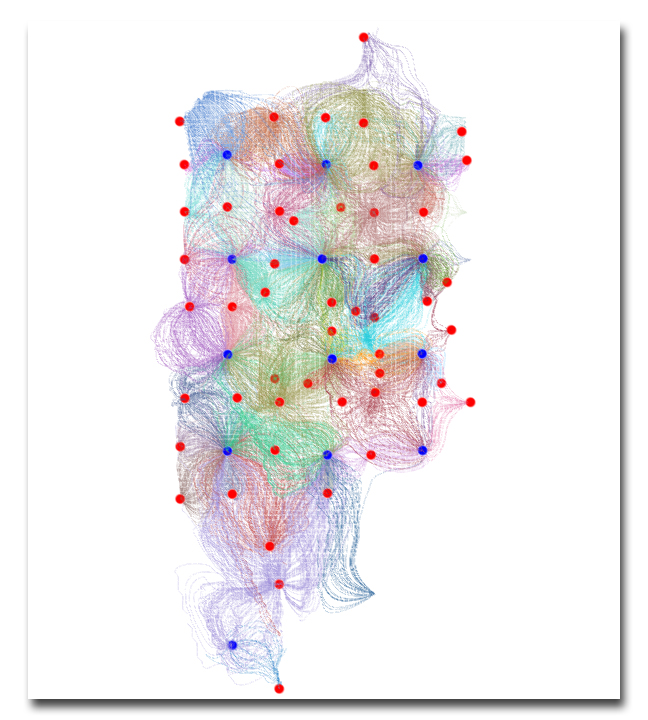
Streamlines calculated by 3DSL using the underlying 3D grid with spatial geological properties and (historical) well rates connect injectors and producers.
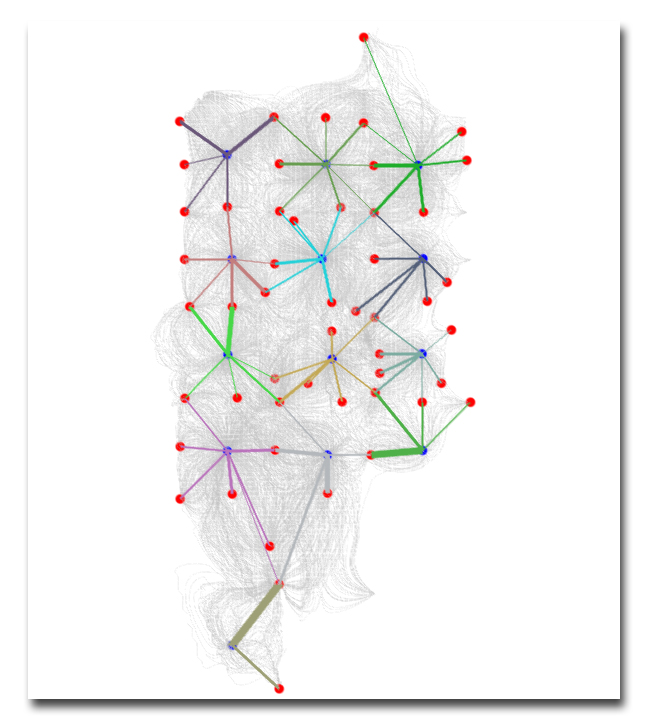
To better represent which wells are connected, injectors and producers are connected by an edge in which color, thickness, and label are used to characterize individual connections.
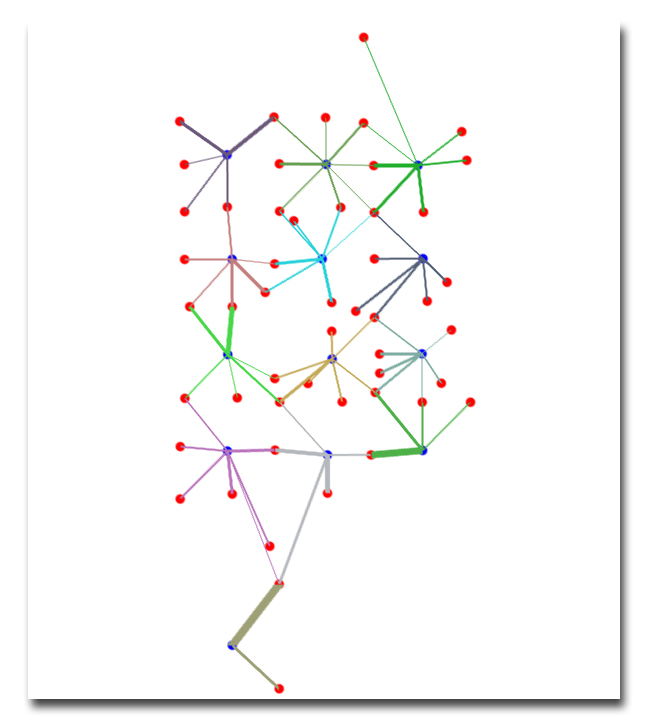
The result is Streamsim's patented Flux Pattern Map (FPmap). Here, all injector-producers connections going to the same injector are colored by the same color making it easy to identify injection patterns.
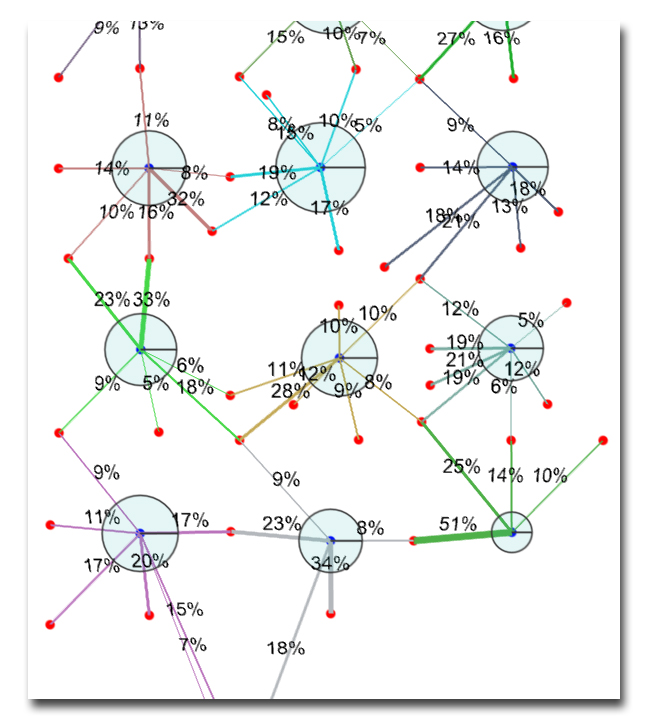
Well allocation factors associate of each edge using the volume rate of the injectors as normalizing value. Colors are associated with injectors. Thickness with the value along each edge.
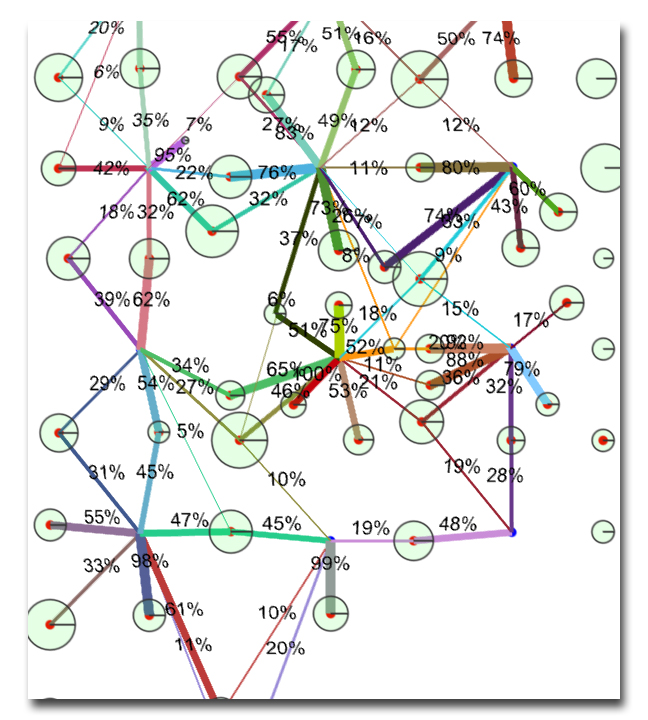
Well allocation factors of each edge using the volume rate of the producers as normalizing value. Colors are associated with producers. Thickness with the value along each edge.
When And Why To Use Streamlines
Streamlines are highly effective for modeling large, geologically diverse, multi-well systems where production primarily depends on fluid injection (such as water,CO2, polymer, etc.). Streamlines are less suitable for scenarios where capillary crossflow, transverse diffusion, or counter-current flow primary role as production mechanisms. Streamlines are recommended for simulating production in mature conventional oil fields undergoing waterflooding, WAG (Water Alternating Gas), and/or enhanced oil recovery (EOR) processes, employing various injector/producer patterns.
The following is a list of reservoir engineering applications where streamlines have shown to be effective.
- Production Surveillance. Quickly identifying and quantifying injector/producer connectivity (well allocation factors) in mature fields is crucial for proactive reservoir management. Streamline tools, such as studioSL, enable the rapid import of production data and well locations from common databases like OFM or geoSCOUT to estimate well allocation factors. Unlike simulation models, a surveillance model functions as a connectivity map and material balance model, making it computationally lightweight.
- Pattern Flooding. Streamlines help identify injector/producer pairs based on the distribution of injection and production volumes across the field, as well as the geological input provided. This enables the quantification of injector/producer efficiency and the assessment of displacement efficiency on a pattern-by-pattern basis.
- Waterflood/Sweep Optimization. With data available on a per-pattern basis, reservoirs can be optimized and proactively managed at the individual pattern level. This capability is a key advantage of streamline-based modeling.
- Screening of Models. Streamline-based reservoir simulation is well-suited for screening large sets of geological models due to its computational efficiency. In heterogeneous systems where geological connectivity is a critical factor, screening with an incompressible waterflood can serve as an effective proxy for more complex displacement processes.
- History Matching. Streamline-based history matching utilizes data from streamlines, such as reservoir volumes "seen" by individual wells and breakthrough times for specific streamlines. This enables selective modification of geological and flow parameters for targeted history matching. It is a powerful technique for achieving effective well-level history matching. Streamsim has extensively researched this approach.
- Uncertainty Quantification. Relying on single models for forecasting does not account for the uncertainty in input data. A more robust approach involves using an ensemble of models for forecasting.

