Classical Approaches to History Matching

History Matching Methods - Overview

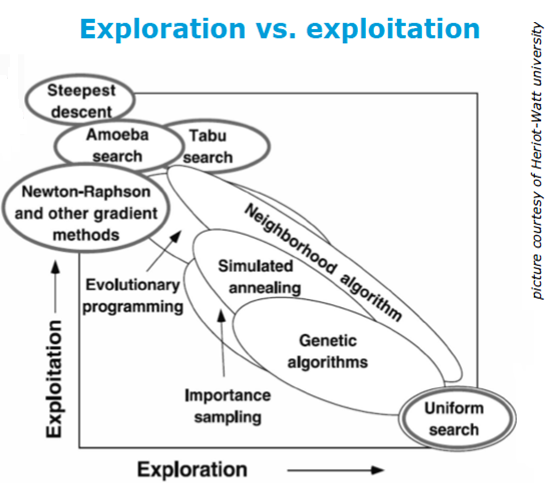
One way of classifying history matching methods is in terms of how the particular methods explore the parameter space versus exploit local regions of the parameter space to find a minimum value of the objective function. The figure on the right describes schematically the various methods which have been applied to history matching problems. In the oil & gas industry, the initial efforts in history matching have principally employed gradient methods (exploitation) which spend computational time finding the single best combination of parameters which minimize the objective function.  Recently however, efforts have switched, and a growing consensus in the oil & gas industry is that methods that emphasize exploration are preferable. The reasons are as follows: It is generally recognized that history matching is a non-unique problem, and that multiple combinations of input parameters can result in an equally-good history match; Exploration methods are designed to find multiple history models; and Multiple history match models are needed for quantification of uncertainty.

Single vs Multiple History Matched Models

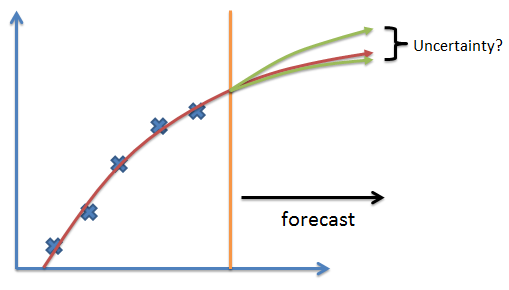
This last point above is very important and should be re-emphasized. Reservoir engineers with experience know that forecasting behavior from a single, history-matched reservoir model is problematic. Accurate forecasting is very challenging for many reservoirs, yet decisions costing the oil company millions of dollars are being made based upon a forecast from a single model. The problem is essentially that one cannot deduce uncertainty from a single model, as shown in the figure below.

What can we say about uncertainty from a single HM model?

 

With a single history-matched model, one cannot know whether the spread in forecasted reservoir response is wide or narrow. When decisions are made based upon a single model, the implicit assumption is that there is zero (or negligible) uncertainty, which may not be correct. Instead of assuming a particular uncertainty spread around a single model, it may be better in many circumstances to dedicate more effort on multiple history matched models using exploration methods, and less effort on exploitation. 

 

Optimization Methods vs Sampling Methods

Given a large amount of time and infinite computer resources for a particular problem, the ideal approach to history matching would be use the sample evenly all possible combinations of parameter values (Uniform Search). In this ideal circumstance, one would create a very large number of reservoir models and compare the reservoir responses with historical data. If the prior model is defined properly (see the discussion on pre-HM screening), one or more history matched models can be defined. This approach describes a very basic (and prohibitively expensive) sampling method, but illustrates the concept of sampling and exploration of the parameter space. Other sampling methods attempt to be more efficient with the computational resources, yet are in general very costly.

Optimization methods sacrifice exploration of the parameter space for exploitation, and therefore (in general) use less computational resources to find history matched models compared to sampling. However, the sacrifice may be that not all the models which match history are found. The risk in this approach is that the reservoir forecasts employed to quantify the uncertainty may be too narrow (under-estimation of uncertainty) compared to a sampling procedure. The degree of under-estimation of uncertainty is rarely ever known.

Optimization Methods in History Matching

All optimization methods have the following requirements:

• Reservoir modeling workflow, automated to reconstruct the model and evaluate the reservoir model response
• Parameterization of the modeling workflow
• Definition of objective function, which compares the reservoir model response to historical data

Selection of the parameters, objective function, and workflow are subjective decisions by the reservoir team, and are an integral part of history matching, uncertainty quantification, and decision making.

Ensemble Kalman Filter

Ensemble Kalman Filter (EnKF) methods have received a tremendous amount of attention in the research literature.  EnKF uses an ensemble of reservoir models (>100) to calculate covariances between the model input parameters and the model responses.  One way of considering these covariances is as gradients, which are then used to minimize an objective function.  The advantages of EnKF methods is that they can modify inter-well petrophysical properties (normally done in the model refinement step), and account automatically for correlations between parameter and response.  In addition, multiple history matched models are created through this procedure.  There are several potential limitations to EnKF.  EnKF methods are:

• Non-trivial to implement and generalize in a robust software
• Prone to ensemble “collapse” (artificial reduction in uncertainty)
• Prone to overshoot (excessively low/high permeability values)
  • Resimulation is required after model update to ensure that dynamic response remains physical
• Susceptible to spurious correlations between parameters and parameters and responses
• Capable of rendering non-Gaussian distributions "Gaussian” during model updates
• Theoretically ideal for linear models, yet reservoir model responses are non-linear

Sampling Methods for History Matching

As described above, sampling methods are very computationally costly, yet theoretically are very rigorous and fit perfectly into the framework of uncertainty quantification.  Many procedures have been proposed to reduce the CPU requirements, such as response surfaces.

References

Stochastic algorithms

• Schulze-Riegert et al., “Evolutionary Algorithms Applied to History Matching of Complex Reservoirs”, SPE 77301
• Mohamad, L. et al., “Comparison of Stochastic Sampling Algorithms for Uncertainty Quantification”, SPEJ March 2010

Gradients

• Roggero, F., and Hu, L-Y., "Gradual Deformation of Continuous Geostatistical Models for History Matching", SPE 49004, SPE ATCE 1998
• Hoffman, B.T., et al., "A Practical Data-Integration Approach to History Matching: Application to a Deepwater Reservoir", SPEJ Volume 11, Number 4
• Gervais, V., et al., "Joint History Matching of Production and 4D-Seismic Related Data for a North Sea Field Case", SPE 135116, 2010 SPE ATCE
• Grana, D., et al., "Single Loop Inversion of Facies From Seismic Data Using Sequential Simulations And Probability Perturbation Method", 2011 SEG Annual Meeting,

Sampling and Response surface methods:

• Wikipedia:  http://en.wikipedia.org/wiki/Markov_chain_Monte_Carlo
• Yang, Z., and Srinivasan, S., "Markov Chain Monte Carlo for Reservoir Uncertainty Assessment", Canadian International Petroleum Conference,2003
• Slotte, P.A., and Smorgrav, E., “Response Surface Methodology Approach for History Matching and Uncertainty Assessment of Reservoir Simulation Models”, SPE 113390, 2008 Europec

Ensemble Kalman filter

• Aanonsen S. et al.,“The Ensemble Kalman Filter in Reservoir Engineering – A Review”, SPEJ Sept. 2009

Case studies:

• Gruenwalder, M. et al., “Assisted and Manual History Matching of a Reservoir with 120 wells, 58 Years Production History and Multiple Well Recompletions”, SPE 106039
• Al-Shamma, B.R. and Teigland, R., “History Matching of the Valhall Field Using a Global Optimization Method and Uncertainty Assessment”, SPE 100946
• Rivera, N. et al., “Static and Dynamic Uncertainty Management for Probabilistic Production Forecast in Chuchupa Field, Columbia”, SPEREE Aug. 2007
• Elrafie, E. et al., “Innovative Simulation History Matching Approach Enabling Better Historical Performance Match and Embracing  Uncertainty in Predictive Forecasting”, SPE 120958